Момент инерции и момент сопротивления
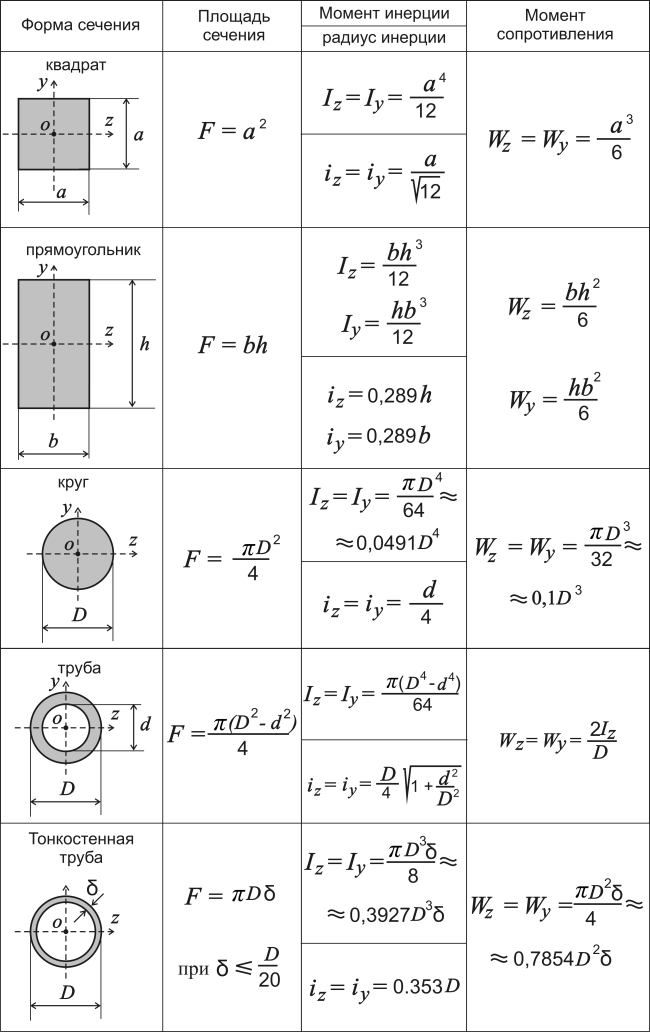
При определении сечения строительных конструкций очень часто необходимо знать момент инерции и момент сопротивления для рассматриваемого поперечного сечения конструкции. Что такое момент сопротивления и как он связан с моментом инерции изложено отдельно. Кроме того, для сжимаемых конструкций также нужно знать значение радиуса инерции. Определить момент сопротивления и момент инерции, а иногда и радиус инерции для большинства поперечных сечений простой геометрической формы можно по давно известным формулам:
Таблица 1. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм.
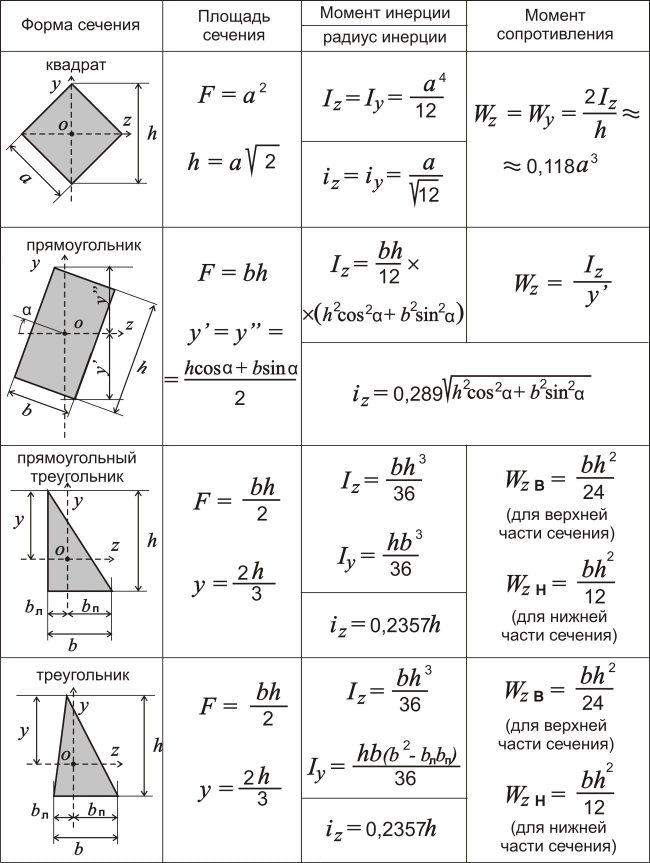
Обычно, этих формул достаточно для большинства расчетов, но случаи бывают всякие и сечение конструкции может быть не такой простой геометрической формы или положение осей, относительно которых нужно определить момент инерции или момент сопротивления, может быть не таким, тогда можно воспользоваться следующими формулами:
Таблица 2. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций более сложных геометрических форм
Как видно из таблицы 2, высчитывать момент инерции и момент сопротивления для неравнополочных уголков достаточно сложно, да нет в этом необходимости. Для неравнополочных и равнополочных прокатных уголков, а также для швеллеров, двутавров и профильных труб есть сортаменты. В сортаментах значения момента инерции и момента сопротивления приводятся для каждого профиля.
Таблица 3. Изменения моментов инерции и моментов сопротивления в зависимости от положения осей.
Формулы из таблицы 3 могут понадобиться для расчета наклонных элементов кровли.
А еще у Вас есть уникальная возможность помочь автору материально. После успешного завершения перевода откроется страница с благодарностью и адресом электронной почты. Если вы хотите задать вопрос, пожалуйста, воспользуйтесь этим адресом. Спасибо. Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Кошелек webmoney: R158114101090
Было бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно
В принципе все предельно ясно, но здесь проще www.kataltim.ru
требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву «Ш». не получается найти какую либо информацию. буду признателен за какую нибудь информацию
Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона» (http://doctorlom.com/item249.html)
там в частности определяется момент инерции тоже не совсем простого сечения.
Вот здесь http://otvet.mail.ru/question/33111076
дана другая формула для момента сопротивления трубы, а именно: W=(D^3-d^3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).
Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.
Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.
Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).
Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).
Неравноплечий уголок.При вычислении Wy не y,а H-y
Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.
Для треугольников при вычислении Wzп h в квадрате.
Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.
Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!
Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.
здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
Игорь, я отправил вам письмо.
Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.
Посмотрите статью «Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.13330.2011», там все достаточно подробно расписано.
Здравствуйте пожалуйста подскажите почему Ql^2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения
История понятия «инерция»
До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.
Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.
Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.
Термин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».
Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов. Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».
Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.
Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.
Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.
Посмотрим на второй закон Ньютона.
Чаще его записывают в виде:
так как в инерциальной системе отсчета сила является причиной ускорения тела.
Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).
Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).
Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.
Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).
Из-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.
Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.
Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.
Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):
Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:
Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Момент инерции
Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Ну а со спинерами и волчками знакомы многие.
Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.
Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

При этом кинетическая энергия вращающегося тела примет вид:
Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.
Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:
Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.
Пример.
Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r1 
В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.
При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.
Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:
Тогда для кинетической энергии поступательного движения будет справедливо отношение:
Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Вопросы
1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i

2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?
3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?