Главная страница > Архитектурный Блог — стр 1 > Архитектурный Блог — стр4 > Платоновы тела и первоэлементы
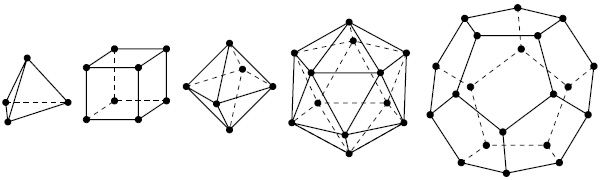
Платоновы тела — это совокупность всех правильных многогранников, объемных (трехмерных) тел, ограниченных равными правильными многоугольниками, впервые описанных Платоном. Им также посвящена заключительная, XIII книга «Начал» Платонова ученика Евклида. При всём бесконечном многообразии правильных многоугольников (двумерных геометрических фигур, ограниченных равными сторонами, смежные пары которых попарно образуют равные между собой углы), существует всего пять объемных П. т., в соответствие которым со времен Платона ставятся пять стихий мироздания: тетраэдр, куб, октаэдр, икосаэдр, додекаэдр.
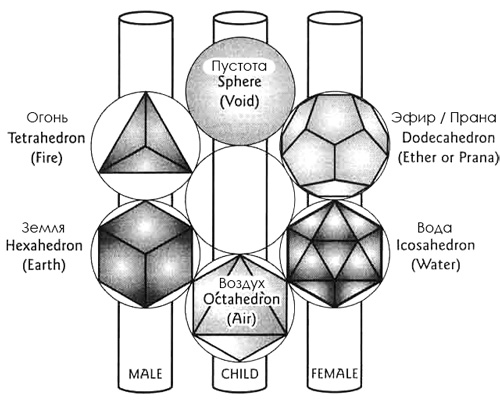
Знание о первоэлементах было доступно древним восточным культурам, таким как индийская и китайская. Платон, а также пифагорейцы, тщательно изучили философские, математические и магические аспекты правильных выпуклых многогранников. Согласно древним знаниям, каждый из этих многогранников соответствует определенной стихии мироздания (первоэлементу) и концентрирует ее энергию. Вершины многогранников излучают энергию, а центры граней поглощают. Ниже дана иллюстрация связи Платоновых тел и первоэлементов из книги Друнвало Мельхиседека «Древняя тайна цветка жизни» :
Далее рассмотрены энергетические характеристики многоугольников с точки зрения китайского учения «У-cин». Зная иньский или янский характер излучения многогранников, а также энергии их стихий, доктора китайской медицины могут оперировать ими как средствами, гармонизирующими энергию человека.
● Гексаэдр (куб) имеет 8 излучающих энергию точек-вершин и 6 граней, в которых происходит поглощение энергии. Так как излучающих точек больше, чем поглощающих, то в соответствии с китайским учением «У-Син» куб относится к мужскому принципу «Ян».
● У октаэдра существует 6 точек-вершин излучения и 8 граней поглощения. Следовательно, октаэдр поглощает больше энергии, чем излучает, поэтому он относится к женскому началу «Инь».
● Тетраэдр имеет 4 вершины и 4 грани, что приводит к равенству «Инь-Ян».
● У икосаэдра 12 вершин и 20 граней, имеющих вид правильных треугольников, поэтому он выражает принцип «Инь».
● Додекаэдр имеет 20 вершин и 12 граней и поэтому он выражает принцип «Ян». Его 12 граней имеют форму правильных пятиугольников.
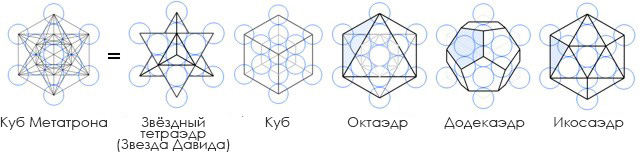
Согласно Мельхиседеку, существует связь между Платоновыми телами из » Цветком жизни «, точнее, они сокрыты в Кубе Метатрона , который заложен в Цветке жизни. В этой статье я дам лишь немного информации из этой книги для ознакомления. Тема эта очень сложна и обширна, но если вы захотите её изучить подробно, книга «Древняя тайна цветка жизни» доступна в интернете.
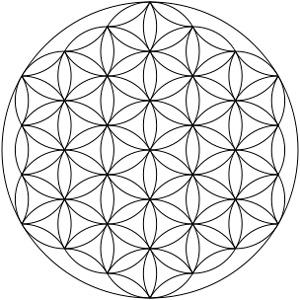
Цветок жизни — это современное название геометрической фигуры, состоящей из нескольких расположенных равномерно, одинаковых окружностей, которые образуют рисунок с шестикратной симметрией, как у Гексагона (шестигранника). Это древнейший символ сакральной геометрии, известный многим древним культурам по всей Земле, изображающий, как полагают, основную форму существования пространства и времени:
Цветок жизни — двухмерное изображение — является символом, проекцией трёхмерной фигуры. И в этой трёхмерной фигуре сокрыт Куб Метатрона:
Куб Метатрона, вписанный в Цветок жизни.
Куб Метатрона соответственно также является не плоской фигурой, а трёхмерным телом. Если соединить линиями все центры шаров Куба Метатрона, то эти линии будут гранями пяти Платоновых тел:
Тетраэдр, вписанный в Куб Метатрона.
Куб, вписанный в Куб Метатрона.
Октаэдр, вписанный в Куб Метатрона.
Икосаэдр, вписанный в Куб Метатрона.
Додекаэдр, вписанный в Куб Метатрона.
!Материалы из статьи могут быть использованы только с активной ссылкой на сайт-источник!
Платоновы тела
Круг деленный на равные части, позволяет нам построить «идеальные» или правильные многоугольники. Полученных правильных многоугольников может быть бесконечно много.
Простейшим правильным многоугольником можно считать равносторонний треугольник.
Но, многогранников, геометрических тел, получиться бесконечно много не может, так как многогранники, это фигуры, полученные соединениями многоугольников, таким образом, при котором, каждая сторона одного многоугольника является так же и стороной другого многоугольника (называемого смежным). Причем, каждая вершина полученного тела, образует соединения граней многоугольников, обладающих ребрами — сторонами и вершинами.
Многогранников в круге (то есть, объемных геометрических фигур), может получиться только пять. Платон соотнес полученные тела со Стихиями следующим образом.
1. ОГОНЬ — Тетраэдр. Состоит из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180;.
Количество граней – 4, вершин – 4, рёбер — 6
Объем — V= (a;;2)/12.
Площадь поверхности — S= a;;3
С точки зрения астрологии, 180 градусов, это аспект оппозиция. В которой одно начало преобразовывает другое, на свое усмотрение.
Стихии Огонь свойственно проявлять свой потенциал в устоявшуюся среду и достигать поставленных целей. Янская, внешняя стихия проявляет себя внутренним противоречием индивидуальности с целым, Иньскими качествами, свойственными стихии Земля.
2.ВОЗДУХ — Октаэдр. Имеет вид двух совмещенных треугольников, соединенных по основанию. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине 240;.
Количество граней – 8, вершин – 6, рёбер – 12
Объем — V= (a;;2)/3.
Площадь поверхности — S= 2a;;3
С точки зрения астрологии, 240 градусов, это аспект тригона.
Воздух совершает беспрепятственную экспансию. Быстро или медленно, но без преодоления и преобразования среды, в которую совершает вхождение. Он воспринимается желанно и благоприятно. Янская внешняя стихия, проявляет качества, свойственные стихии Вода.
3. ЗЕМЛЯ — Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат.
Куб состоит из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270;.
Количество граней – 6, вершин – 8, рёбер – 12
Объем — V= a;.
Площадь поверхности — S= 6a;
С точки зрения АСТРОЛОГИИ, 270 гр представляет динамичный аспект квадратуры.
Поверхностное противоречие между Стихией и свойством аспекта легко разрешимо, если учитывать, что существует внешний и внутренний уровень. Инь и Ян.
Так — Огонь, обладает стабильным и статичным аспектом. Янская стихия проявляется Иньским образом.
Потенциал Огня столь велик, что после его проявления реальность не может остаться прежней. Ей приходится выстраивать новые центры тяжести, искать новые способы существования и подстраиваться под трансформации, вызванные Огнем.
После проявления Огня, противоречие не устранимо, оно постоянно. Оно не влияет на саму стихию Огонь, только среда, в которой проявляется Стихия, испытывает ее влияние и примеряется к ней, подстраивается под нее. Проявившаяся стихия Огонь, имеет Иньские — длительные следствия.
Проявившаясь стихия Земли, своим устойчивым и статичным потенциалом в силу медленного движения не повреждает среду, но заставляет ее приспосабливаться и искать способы взаимодействия, в которых среда проявляет Янские качества.
4. ПРОСТРАНСТВО (Эфир) — Додекаэдр — двенадцатигранник — правильный многогранник, составленный из двенадцати правильных пятиугольников. Додекаэдр имеет центр симметрии и 15 осей и 15 плоскостей симметрии.
Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324;.
Количество граней – 12, вершин – 20, рёбер – 30
Объем — V= a;(15+7;5)/4.
Площадь поверхности — S= 3a;;5(5+2;5)
С точки зрения астрологии, Пространство порождает творческий минорный, дискретный аспект с углом в 36 (72, 144) градусов — Дециль/Полуквинтиль, обладающий природой неожиданной, творческой динамики, оказывающей влияние на среду. Считается, что это аспект «гуманности», соразмеренности и уместности инициатив.
Он тактично встраивает индивидуальное в целое.
5. ВОДА — Икосаэдр — двадцатигранник. Каждая из 20 граней представляет собой равносторонний треугольник. 30 ребер, 20 граней и 12 вершин. Икосаэдр имеет 59 звездчатых форм.
Каждая вершина икосаэдра является вершиной пяти треугольников, сумма плоских углов при каждой вершине равна 300;.
Количество граней – 20, вершин – 12, рёбер – 30
Объем — V= 5a;(3+;5)/12.
Площадь поверхности — S= 5a;;3
С точки зрения астрологии, это аспект секстиля, отличающийся кратковременным интенсивным взаимодействием среды и индивидуальности.
(Чем короче «ребро», тем длительней взаимодействие, чем больше вершин, тем больше пиков активности.)
Иньская, скрытая, внутренняя Стихия порождает Янский способ взаимодействия на внешнем уровне, качествами проявления более соответсвующий стихии Воздух.
_____________________________
«В тот день, когда наука начнет изучать не только физические явления, она достигнет большего прогресса за одно десятилетие, чем за все предыдущие столетия своего существования.» — Никола Тесла.
Существует множество примеров случайных совпадений.
Но, совпадений не может быть от природы, так как, может случиться только то, что пребывает в резонансе, симметрии, кратности — во взаимодействии.
Числовых «Совпадений» столь много, что становится очевидной их не случайность.
Каждый может найти их самостоятельно, вот несколько примеров данной
занимательной абстракции:
Динамичность взаимодействия Стихий в градусах:
Вода — Огонь 300-180=120;
Воздух — Огонь 270-180=90;
Вода — Воздух 300-240=60;
Вода — Земля 300-270=30;
Воздух- Земля 270-240=30;
Сложим суммы плоских углов полученных многогранников
ОГОНЬ, Тетраэдр 180;
ВОЗДУХ, Октаэдр 240;
ЗЕМЛЯ, Куб 270;
ВОДА, Икосаэдр 300;
Пространство, Додекаэдр 324;
180+240+270+300+324=1314;. Разделим на 360; окружности.
1314:360=3,65
365 дней в году.
Температура человеческого тела 36,5 градусов.
324-180=144
24 часа умножим на 60 минут=1440.
60минут умноженное на 60 секунд =3600, 360 градусов в окружности.
Сложим вершины многоугольников: 4+6+8+12+ 20=50
360:50=72
72 часа в трех сутках.
72 удара в минуту средний пульс здорового взрослого человека.
Угол вращения цепочки ДНК =72.
72 — итог сложения всех букв, вписанных в тетраграммматон.
72 — максимальное число сфер, касающихся одной сферы в плотной упаковке в 6-мерном пространстве.
В исламе и иудаизме есть понятие 72 имени Бога.
72 градуса — внешний угол правильного пятиугольника
Если исключить из расчетов Пространство, то 360:30=12.
12 знаков Зодиака
12 месяцев в году и так далее.
180+240+270+300=990;
990:360=2,75
Средний срок беременности составляет 275 суток.
Нумерология, считает, что число 275 — союз Бога с человеком во имя творчества.
Правильные многогранники можно вписывать друг в друга.
По этому, все Стихии могут проявляться как на внешнем, так и на внутреннем уровне.
Додекаэдр, ПРОСТРАНСТВО, содержит в себе все фигуры.
В куб вписывается тетраэдр — ОГОНЬ, аналогичным образом в тетраэдр вписывается куб.
Стихия Огонь пребывает в недрах планеты Земля, а так же, Огонь может проявляться над Землей в виде света, молний и тепла.
Октаэдр — ВОЗДУХ, может быть вписан в куб, а так же, куб может быть вписан в Октаэдр.
Стихия Воздух содержится в пустых полостях планеты Земля, а так же, вокруг Земли.
В куб можно вписать икосаэдр. Воде свойственно заполнять пустые полости Земли.
В икосаэдр можно вписать додекаэдр и, следовательно, куб и тетраэдр.
Стихия Вода способна связывать между собой все Стихии.
Она пребывает и на поверхности Земли, и в Воздухе, выделяется из Воздуха в процессе горения, так же, она, как и все фигуры способна пребывать в Пространстве, Эфире.
АКТУАЛЬНОСТЬ ПЛАТОНОВЫХ ТЕЛ В СОВРЕМЕННОЙ АРХИТЕКТУРЕ И СТРОИТЕЛЬСТВЕ Михеенкова Е.С.,Смирнова В.И.
Московский государственный технический университет имени Н.Э. Баумана
ISSN (печатный вариант): 2073-0071
Ключевые слова
геокупол, многогранник, строительство, энергоэффективность, архитектура, geodesic dome house, polyhedron, building, energy efficiency, architecture
Просмотр статьи
⛔️ (обновите страницу, если статья не отобразилась)
Ваш браузер не поддерживает фреймы
Аннотация к статье
Статья посвящена применению правильных многогранников, известных с древнейших времен, для проектирования новейших зданий. Особое внимание уделено разработке, совершенствованию и многоцелевому использованию геодезических куполов, созданных на основе Платоновых тел, в современном мире. Авторы анализируют достоинства и недостатки различных геометрических архитектурных форм, которые возникают при возведении жилых и производственных помещений.
Текст научной статьи
Правильным многогранником называется выпуклый многогранник, все грани которого — правильные и равные между собой многоугольники и все многогранные углы которого правильны и равны между собой (т.е. все вершины, ребра, грани, двугранные углы многогранника равноправны). Первое письменное упоминание о правильных многогранниках принадлежит грекам. Пифагорейцам были известны тетраэдр, куб и октаэдр. Описание додекаэдра и икосаэдра приписывается — Теэтету Афинскому (начало четвёртого века до н.э.) По-видимому, он же доказал, что других правильных многогранников не существует. Наиболее известное описание правильных многогранников позже было изложено в трудах Платона. Именно поэтому они часто называются платоновыми телами. В его трактате «Тимей», написанном около 360 г. до н.э., рассматриваются физические свойства Вселенной — какой она представлялась древним грекам, и составляющие ее первоэлементы, приводятся конструкции четырёх многогранников (Рис.1) и говорится, что они олицетворяют четыре стихии: тетраэдр (а) это огонь, гексаэдр (куб) (б) — земля, октаэдр (в) — воздух, икосаэдр (г) — вода. Додекаэдр (д), согласно Платону, символизирует Вселенную. Рис. 1 Построению и свойствам 5 правильных многогранников (а также доказательству того, что других не существует) посвящена тринадцатая — заключительная — книга «Начал» Евклида. Согласно комментарию неоплатоника Прокла, структура «Начал» соответствует устройству Вселенной по Платону: она начинается с самых исходных элементов — точек и прямых — чтобы в результате прийти к построению мира в целом. Изучение многогранников, углубленное знание пространственных фигур дает возможность применения их в архитектуре, строительстве и искусстве. Есть очень много зданий, которые используют куб как основную форму. Одним из наиболее ярких примеров может служить постройка Хабитат 67 архитектора Моше Сафди, возведенная в 1967г в Канадском Монреале (Рис.2). Рис. 2 Пирамида (в архитектуре) — монументальное сооружение в форме пирамиды, обычно относящееся к Древнему миру. К крупным пирамидам относятся египетские пирамиды (самые древние из всех) и пирамиды доколумбовых культур (ацтеки, майя) в Латинской Америке. Однако и в современной архитектуре встречаются спорные шедевры, смоделированные на основе тетраэдра. Стеклянная пирамида Лувра во дворе Наполеона служит главным входом в Лувр и является одним из символов Парижа. Примечателен и Офис Словацкого радио (так называемая «Братиславская пирамида») в виде перевернутой пирамиды (рис. 3а). Здание было построено в 1969-1984 гг., арх. Ш. Дюркович, Б. Кислинг и Ш. Светко. А в 2006 году, к ним присоединилась еще одна пирамида, которую некоторые уже называют Восьмым чудом Света. Речь идет о Дворце Мира и Согласия в Астане, созданном всемирно известным архитектором Норманом Фостером для проведения «Конгресса лидеров мировых и традиционных религий» (Рис. 3б). Рис. 3 (а,б) Однако хотелось бы более подробно рассмотреть применение в архитектуре икосаэдра. Важной его особенностью является оптимально-распределенное расположение вершин и граней, стремящихся к идеальной сфере (рис. 4). Путем триангуляции икосаэдра или иного правильного многогранника, приближаясь к сферической поверхности, мы получаем конструкцию, известную как геокупол (геодом, геодезический купол). И из всех тел Платона именно икосаэдр в строительном применении требует наименьших затрат труда и материалов для покрытия наибольшей полезной площади и при этом обладает наилучшими прочностными характеристиками. Правильный многогранник Число граней Форма граней Тела Платона Площадь поверхности Тетраэдр 4 Огонь Гексаэдр 6 Земля Октаэдр 8 Воздух Икосаэдр 20 Вода Додекаэдр 12 Вселенная Рис. 4 Первым геодезическим куполом (на основе икосаэдра) стал открытый 18 июля 1926 в Йене планетарий им. Цейса, созданный немецким инженером Вальтером Бауэрсфельдом. Однако истинную революцию в инженерии произвёл Ричард Бакминстер Фуллер, спроектировав пространственную конструкцию «геодезического купола». В 1942 году Б. Фуллер получил патент на изобретение более верной проекции сферической поверхности на плоскость. Идея достаточно проста, сфера представляется в виде икосасаэдра, то есть двадцатигранника со сторонами в виде правильных треугольников. Но самое известное использование икосаэдра, вероятно, Павильон США на Экспо-67, ныне музей «Биосфера», внутри которой сегодня располагается музей, посвященный охране окружающей среды, в Монреале, Канада (рис. 5). Строение носит название Биосферы Фуллера. Структура построения геодезической сетки не является хаотичной, а представляет собой строгую математическую модель. Хотя ни вершины многогранника, ни центры граней не обязательно находятся на одном расстоянии от центра, однако эти условия приближенно выполняются. Эта модель берет свое начало как раз из геометрии Платоновых тел — правильных многогранников, открытых учеными еще в далеком прошлом. Рис. 5 Концепция, благодаря которой была создана эта конструкция, еще не получила достаточную известность. Поскольку в основе большинства куполов лежит икосаэдр (20-гранник, каждая грань которого представляет собой равносторонний треугольник), то он и задает нам первичное равномерное деление сферы на 20 одинаковых сферических треугольников. Эта фигура и разворачивается на плоскость, давая практически неискаженные соотношения по всей поверхности [3,280]. Основываясь на параметрах стороны икосаэдра, сфера делится в зависимости от выбранного класса и частоты деления (рис. 6). Количество рёбер, формирующих поверхность купола, называется частотой деления сферы геодезическими линиями (триангуляция). Обозначают её латинской буквой «V». Другими словами, это степень сферичности изначального многогранника. Рис. 6 Преимущества геокупола (купольного дома) многочисленны: 1. Энергоэффективность. Внешняя площадь купола почти на треть меньше, чем у параллелепипеда с такой же жилой площадью, то есть при одинаковой площади основания экономия на строительных материалах около 30% по сравнению с обычным домом. Площадь поверхности, подверженной влиянию окружающей среды, имеет намного больше влияние на энергетическую эффективность, чем толщина стен или качество герметика в стыках. К тому же, некоторые из существующих на сегодняшний день куполов уже оснащены оптимально сориентированными солнечными батареями, ветровыми генераторами и настолько эффективны, что производят энергии больше, чем потребляют. 2. Прочность. Геодезический купол обладает большой несущей способностью, причем, чем больше купол, тем она выше (за счет распределения нагрузки на большее количество элементов конструкции). 3. Надежность. Геодезический купол не имеет внутренних несущих стен, является сетчатой оболочкой и поэтому очень легкий, следовательно, снижаются требования к устройству фундамента. Он обладает очень высокой устойчивостью к нагрузкам: до 700 кг снега на квадратный метр, выдерживает порывы ураганного ветра до 250 км/час. 4. Сейсмоустойчивость достигается за счет малого собственного веса и шарнирности всех соединений элементов купола. Благодаря идеальной аэродинамической форме, купола можно возводить в ветреных и ураганных районах. Здания и сооружения такого типа идеальны для возведения и эксплуатации в районах севера с суровым климатом [2,105]. 5. Контроль климата. Чем меньше общая площадь внешней поверхности стен и крыши, тем выше КПД энергозатрат на контроль климата в помещении. Искривленная поверхность внутри купола способствует естественной циркуляции воздуха и эффективному воздухообмену в помещениях. Именно поэтому все древние жилища человека (юрта, вигвам, иглу) имели круглую форму и небольшое отверстие на макушке строения. Натуральные «кольцеобразные» течения воздуха, предотвращают расслоение, и температура воздуха остается одинаковой по всему объему купола, от пола до апекса. Аэродинамический эффект конструкции экономит немалые средства на отоплении и кондиционировании [1,10]. 6. Освещение. Равномерное и экономичное освещение, поскольку возможно размещение в любой части купола «окна — треугольника», что позволяет максимально использовать световой день в помещении. К тому же освещение отличается превосходными характеристиками, так как сферические формы усиливает свет, в то время как прямоугольные поглощают. 7. Скорость и простота возведения. Этапы строительства не требуют больших временных затрат (установка и обшивка каркаса, утепление, установка кровли, монтаж дверей и окон, окончательная отделка). При этом за счет универсальных единиц сборки не требуется ни сложных подъемных механизмов, ни большого количества рабочих. 8. Уникальная энергетика и уют. Больше свободы планировки (в зависимости от степени сферичности изначального многогранника возникает широкий выбор длины ребер, то есть используемого на практике бруса), индивидуальности интерьера, соборные потолки, равномерное распределения света, тепла и звука, возможность навески разнообразного оборудования на стенах. Равномерность распределения нагрузки по оболочке купола позволяет изъять до 50% треугольников, а ненесущие проемы использовать для свободного обрамления дверей, окон, веранд, балконов, зимних садов. Реализация данного разработанного проекта будет иметь огромный эффект при строительстве домов [5,26]. 9. Экология. Купольные сооружения не наносят вреда окружающей среде и здоровью человека. Поскольку сборные блоки в большинстве куполов относительно малы, то легко использовать более дешевые материалы, и это также снижает экологические издержки. Что касается недостатков, теоретически присущих купольным сооружениям, то в основном они являются оборотной стороной достоинств: 1. Большое количество отходов пиломатериалов, поскольку стандартные продаваемые заготовки имеют прямоугольную форму, а не многогранную. 2. Фундамент должен точно соответствовать периметру стен, и достичь этого сложнее, чем в случае с обычным прямоугольником. 3. Расширить площадь произвольным образом не получится из-за ограничений, накладываемых формой, и нельзя пробить нижние части купола, не ослабив его конструкцию. 4. Кровельные работы — сложны и трудоёмки. Причина кроется в сложной геометрии (линия ската ступенчатая, от почти вертикальной до почти горизонтальной), и ни ветер, ни гравитация не будут защищать от потоков дождевой воды. А большое количество стыков и швов потенциально представляют угрозу протекания. 5. Необходимые для купола изоляционные материалы и окна сложной формы стоят много дороже стандартных аналогов. 6. Возможны сложности с прокладкой электрического кабеля и с размещением водопроводных, дымоходных и канализационных труб и вентиляционных отверстий из-за ограничений, налагаемых формой сооружения, многообразием углов и линейных размеров. 7. Превосходные характеристики циркуляции воздуха могут обернуться нежелательным распространением запахов по всему пространству, стремлением горячего воздуха вверх и соответственно, прохладой в нижней части дома, или накоплением пара в верхней части купола при большой разнице температур внутри и снаружи. 8. Прекрасная акустика приводит к сверхпроводимости и нежелательных шумов тоже. 9. Свобода планировки и меньшее количество традиционно прямоугольных стен вызывает затруднения при расстановке мебели или развешивании привычных предметов интерьера на стенах. Однако нетрудно заметить, что практически все недостатки носят гипотетический характер. На практике эти проблемы легко устранимы при рациональном подходе к проектированию, разумном выборе материалов, профессиональном подходе к конструированию здания и тщательном выполнении работ на всех этапах возведения. В заключение стоит признать, что в настоящее время использование такого типа конструкций чрезвычайно актуально, хотя и уходит корнями своего происхождения в глубокое прошлое. Сегодня геодезические купола используются повсеместно для строительства жилых домов и производственных сооружений: выставочные павильоны, лаборатории, навесы, мастерские, сараи, крыши для стадионов, кортов, бассейнов. За ними прячут сложные элементы радиолокационных станций, спасают от антарктического холода полярные экспедиции. На сегодняшний день актуальна технология строительства купольных коттеджей в качестве экологичного, эргономичного, эстетичного и экономически доступного жилья для санаторно-курортных предприятий в Крыму [4,167]. Геокупол на основе правильного многогранника — один из наилучших вариантов организации пространства, например, для застройки современной технической деревни для людей, работающих в IT-сфере. Геодезический купол — модуль для постройки в космосе гигантских космических станций, непременный элемент проектов освоения Луны и Марса.