Построение сетевого графика
Каждый менеджер проекта сталкивается с такой типовой для него задачей, как построение сетевого графика. В настоящее время этот процесс полностью автоматизирован и, как правило, у менеджера не возникает больших проблем. Уже давно нет необходимости чертить на бумаге графики, высчитывать ранние и поздние начала или окончания задач, соединять задачи стрелками, вычислять длину критического пути. ИСУП успешно решает все эти задачи.
Однако, без понимания основ и правил построения сетевых графиков менеджеры проектов довольно-таки часто совершают ошибки. Несмотря на то, что современные ИСУП достаточно «умные» и подстраховывают менеджера проекта во многих моментах, связанных с расписанием проекта, тем не менее, остаются «слепые» зоны, которые лежат только в зоне ответственности менеджера проекта.
Для того, чтобы получить настоящую пользу от ИСУП, ей надо уметь грамотно пользоваться, как и любым другим инструментом.
Что такое сетевой график
Сетевой график (англ., Project Network) — это динамическая модель проекта, отражающая зависимость и последовательность выполнения работ проекта, связывающая их завершение во времени с учётом затрат ресурсов и стоимости работ.
Сетевой график может быть построен в двумя способами:
Правила построения сетевого граифка
Прежде всего, построение сетевого графика заключается в правильном соединении между собой событий (на схеме обозначаются кружками) с помощью работ (на схеме обозначаются стрелками). Правильность соединения стрелок заключается в следующем:
Исходные работы
Построение графика начинается с изображения работ, не требующих для своего начала результатов выполнения других работ. Такие работы можно назвать исходными, так как все остальные работы комплекса будут выполняться только после их полного выполнения.
В зависимости от специфики планируемого комплекса, исходных работ может быть несколько, а может быть только одна. Размещая исходные работы необходимо учитывать, что на сетевом графике, должно быть только одно исходное событие.
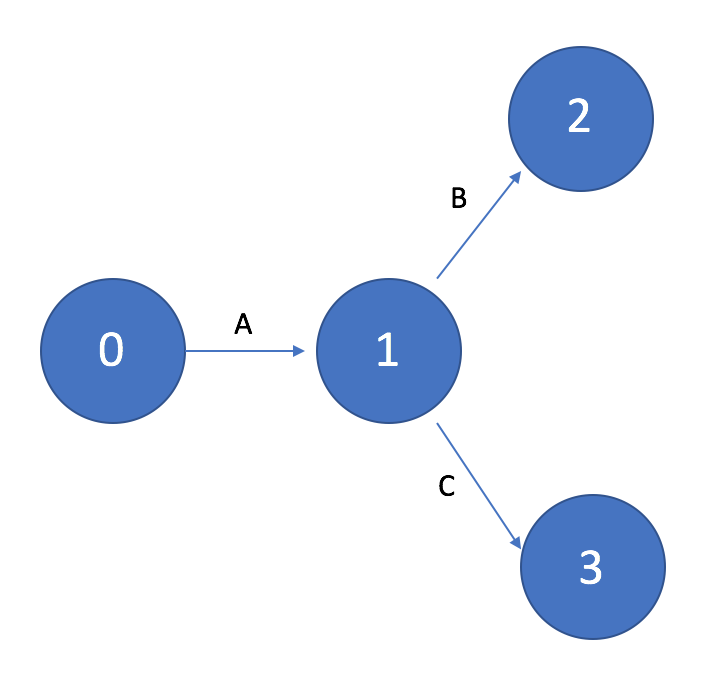
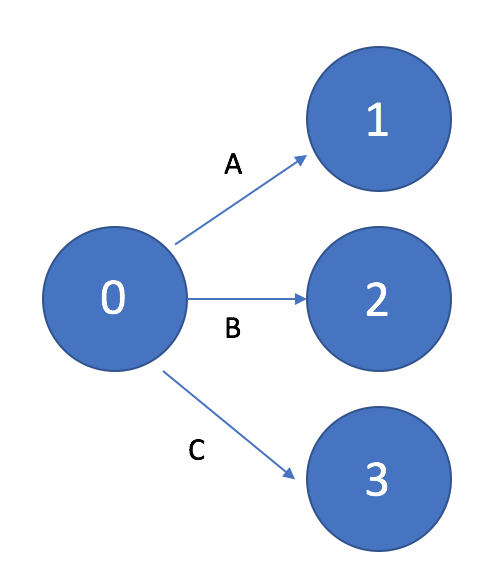
На рисунке 1 показан пример начала сетевого графика с одной исходной работой (работа A), а на рисунке 2 пример начала сетевого графика с тремя исходными работами (работы A, B, C).
Рисунок 1. Сетевой график с одной исходной работой
Рисунок 2. Сетевой график с тремя исходными работами
Последовательные работы
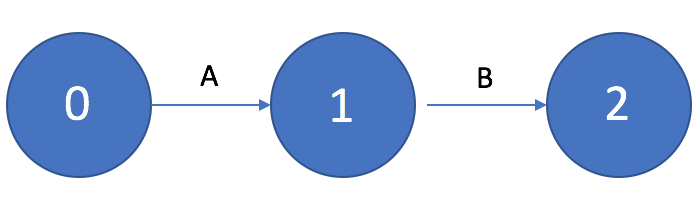
Если работа B должна выполняться только после выполнения работы A, то на графике это изображается в виде последовательной цепочки работ и событий.
Рисунок 3. Последовательно выполняемые работы
Работы, выполняемые после одной и той же работы
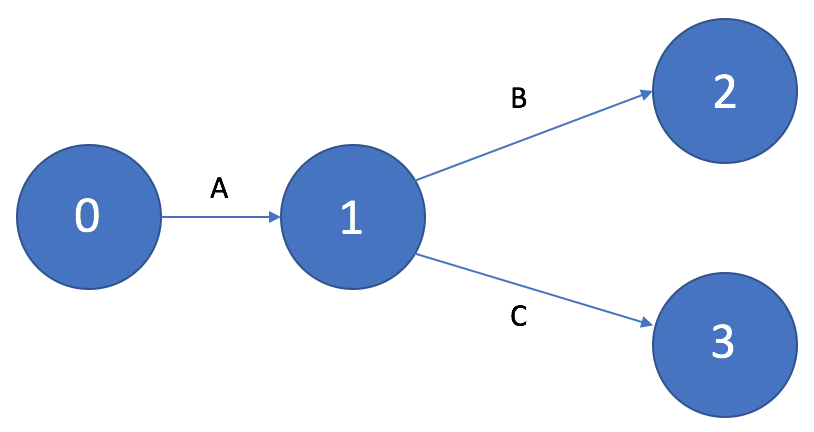
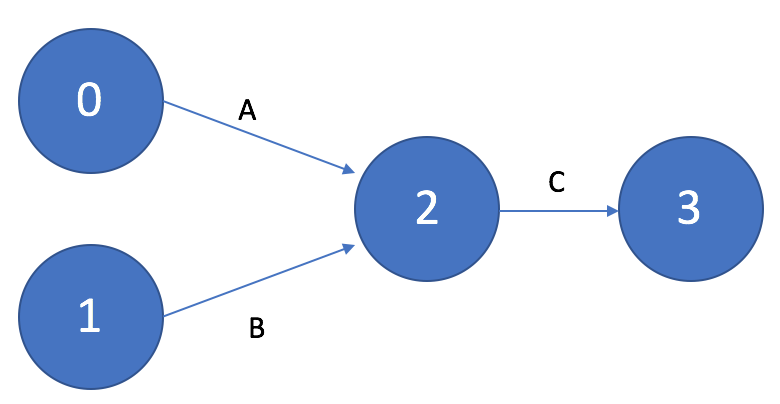
Если для выполнения нескольких работ, например, B и C необходим результат одной и той же работы A, то на графике это изображается «параллельными» стрелками, выходящими из события, являющегося результатом выполнения работы А.
Рисунок 4. Работы, выполняемые после одной и той же работы
Работа, выполняемая после нескольких работ
Если для выполнения работы C необходим результат работ A и B, то на графике это изображается «параллельными» стрелками, входящими в событие, после достижения которого следует работа C.
Рисунок 5. Работа, выполняемая после нескольких работ
Работы, выполняемые после частичного выполнения других работ
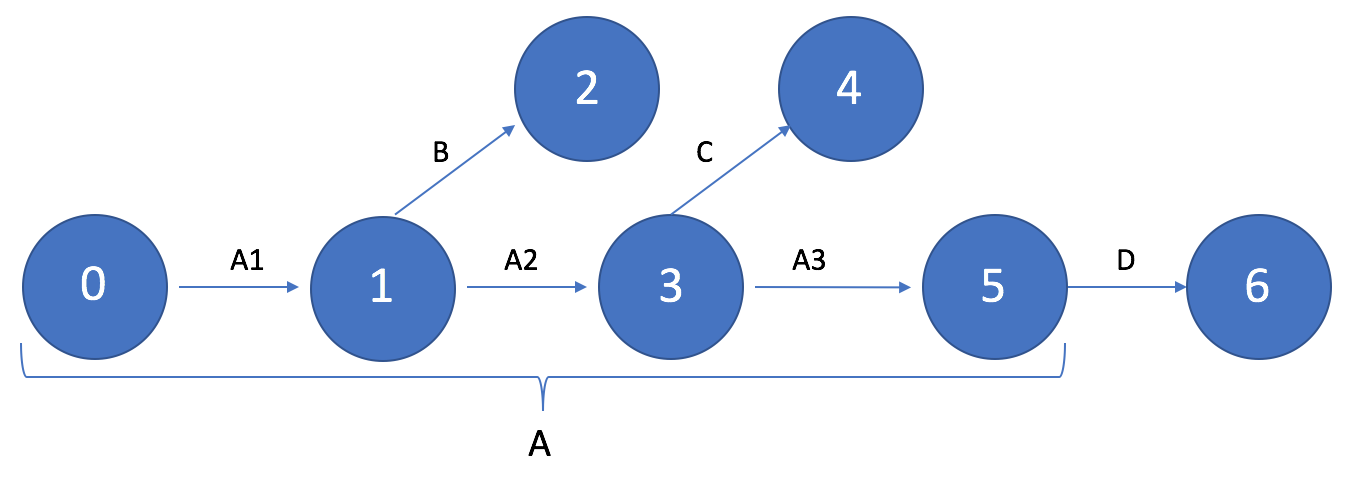
Если для выполнения работ B и C необходим промежуточный результат работы A, то работа A разбивается на подзадачи таким образом, чтобы первая ее подзадача (A1) выполнялась до получения промежуточного результата, необходимого для начала работы B, а вторая подзадача выполнялась до получения промежуточного результата, необходимого для начала работы C, последующая же часть A3, может выполняться параллельно с работами A1 и A2.
Рисунок 6. Работы, выполняемые после частичного выполнения других работ
Работы, имеющие общие начальное и конечное события
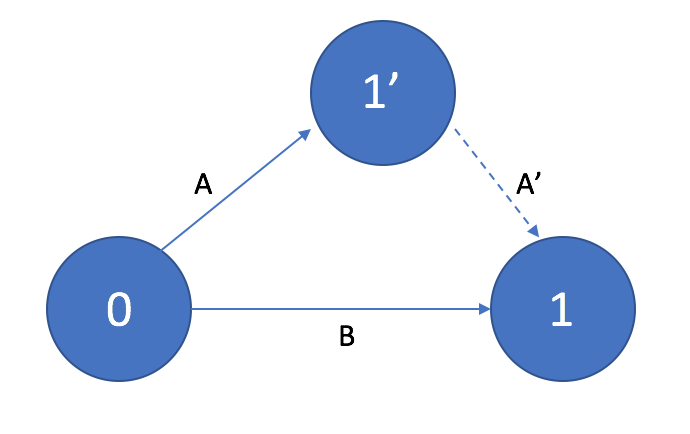
Два соседних события могут быть объединены одной и только одной работой. Для изображения параллельных работ на сетевом графике вводится так называемое промежуточное событие и фиктивная работа.
Рисунок 7. Работы, имеющие общие начальное и конечное события
Использование фиктивных работ
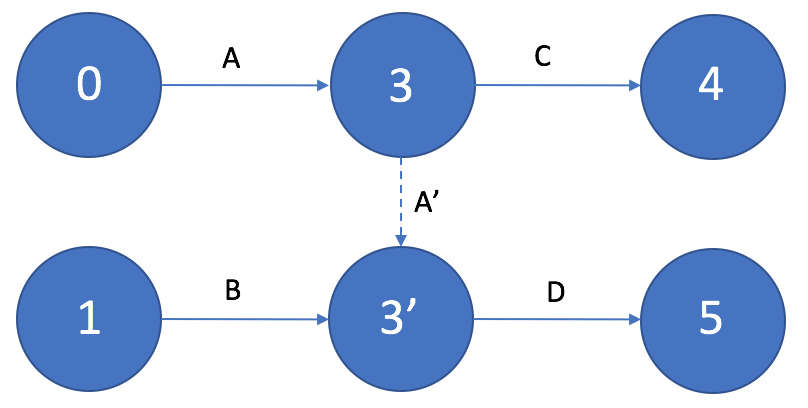
Если выполнение работы D возможно только после получения совокупного результата работ A и B, а выполнение работы C – после получения только результата работы А, то в сетевом графике необходимо ввести дополнительное событие и фиктивную работу.
Рисунок 8. Использование фиктивных работ
«Хвосты» и «тупики»
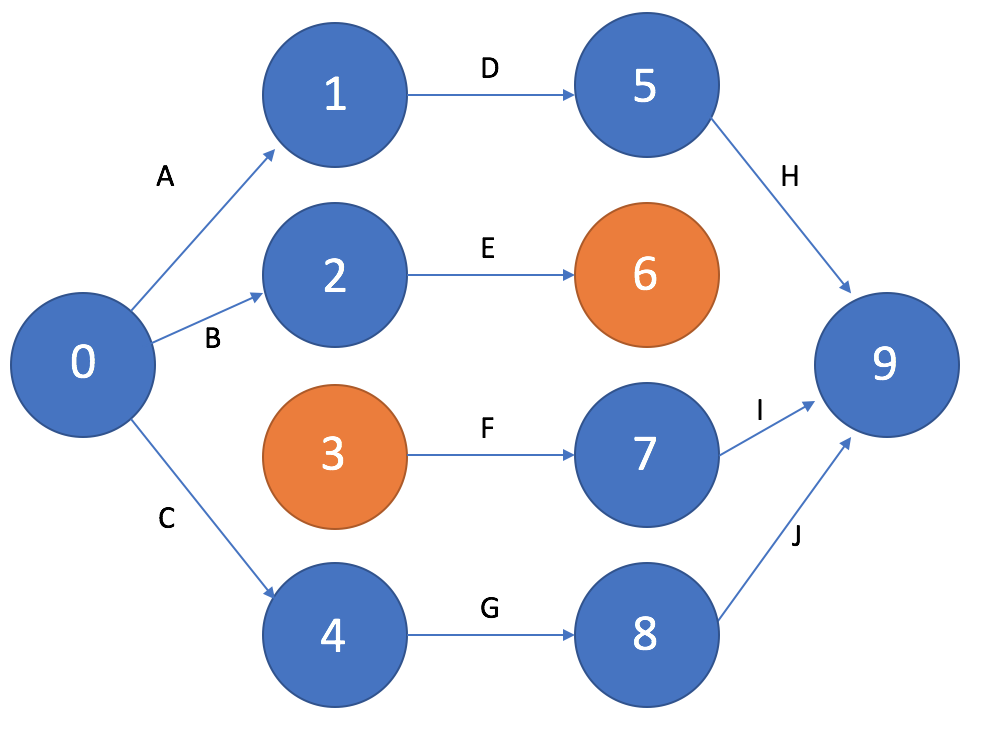
В сети не должно быть «тупиков», т.е. промежуточных событий, из которых не выходит ни одна работа. На рисунке 9 тупиковым событием является событие 6.
Также не должно быть «хвостов», т.е. промежуточных событий, которым не предшествует хотя бы одна работа. На рисунке 9 хвостовым событием является событие 3.
Рисунок 9. «Хвосты» и «тупики» в сетевом графике
Циклы
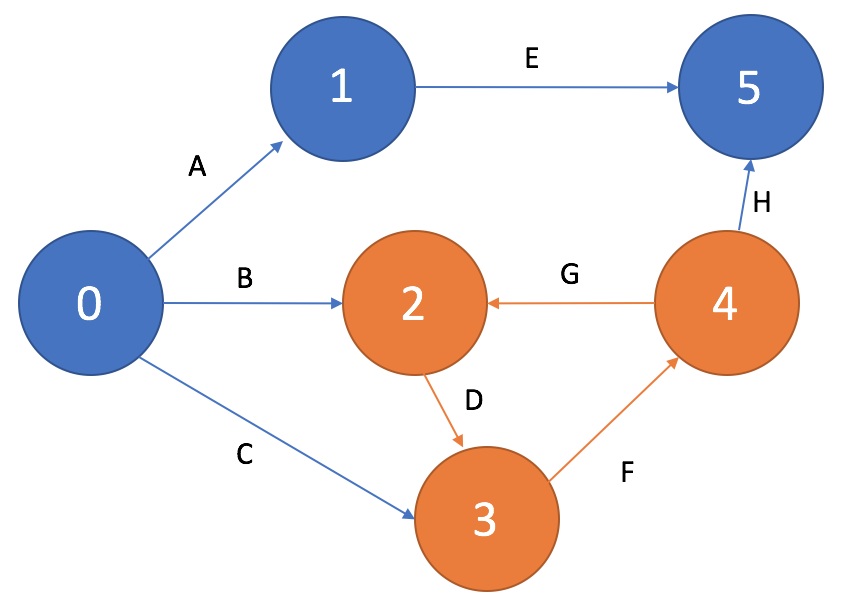
На сетевом графике не должно быть циклов, состоящих из взаимосвязанных работ, создающих замкнутую цепь — цепочка работ D->F->G на рисунке 10. Данная ситуация скорее всего свидетельствует об ошибке при составлении перечня работ и определении их взаимосвязей.
Рисунок 10. Цикл на сетевом графике
В таком случае необходимо проанализировать исходные данные и в зависимости от сделанных по итогам анализа выводов, либо перенаправить работу создающую цикл в другое событие (если работам, начинающимся в этом событии требуется ее результат, или если она является частью общего результата), либо совсем исключить ее из комплекса (если выявлено, что ее результат не требуется).
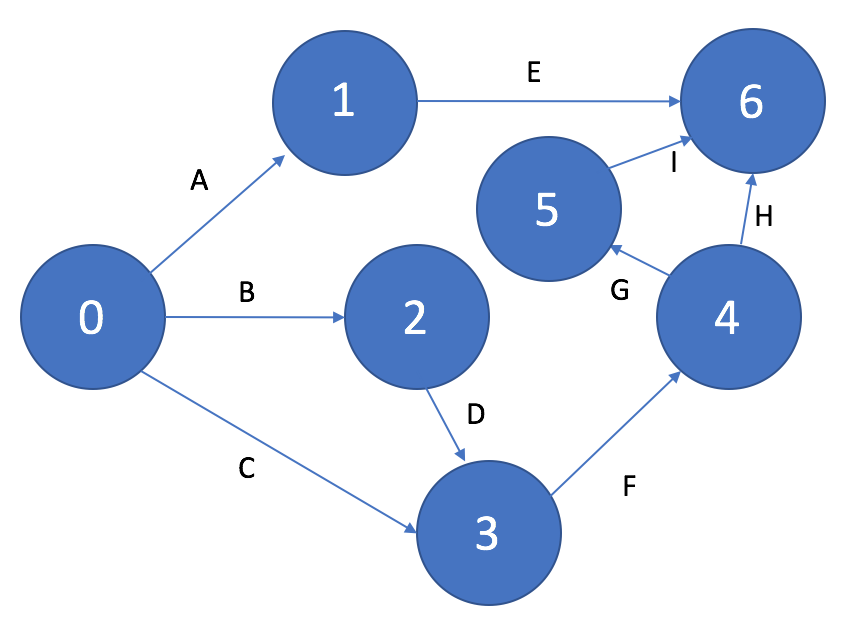
На рисунке 11 приведен пример устранения цикла, когда работа G становится частью общего результата.
Рисунок 11. Устранение цикла на сетевом графике
Именование работ и нумерация событий
Каждая работа в сетевом графике должна определяться однозначно, только ей присущей парой событий, как и не должно быть на графике событий с одинаковыми номерами.
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 0. Из исходного события вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 1. Затем вычеркивают работы, выходящие из события 1, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 2, и так продолжается до завершающего события.
Сетевой график строительства
При разработке сетевого графика (рис. 6) согласно заданию руководителя возможны следующие варианты:
1) безмасштабный сетевой график строительства объекта, рассчитанный секторным методом;
2) сетевой график строительства объекта в масштабе времени с построением оптимизированного графика движения рабочих, эпюры капиталовложений, графика поставки строительных материалов [2].
                 | Рис. 5. Матрица неритмичного потока |
Рис. 6. Пример составления сетевого графика
Сетевой график может быть разработан очень детально на строительные работы по возведению части здания и служить документом оперативного планирования и управления, он может быть рассчитан табличным методом с указанием всех имеющихся частных и общих резервов времени работ.
На основе расчетных данных календарного плана составляют карточку-определитель (табл. 14) и сетевую модель технологии производства СМР, при построении которой соблюдают условия наличия фронта работ, обеспечения строительной техникой, рабочими и правила построения сетевых графиков [3].
Карточка-определитель работ сетевого графика
| № п/п | Шифр работ | Наименование работ | Объем, ед. | Норма времени | Затраты труда, чел.-дн | Требуемые машины | Число смен | Численность рабочих в см | Состав бригады | Продолжительность работы, дн |
| ед. изм. | кол-во | чел.-ч | маш.-ч | наимен. | кол-во | маш.-см |
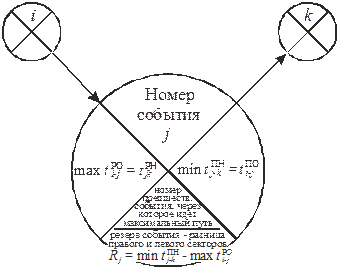
После построения безмасштабную сетевую модель рассчитывают секторным методом (подробнее о секторном методе см. [2]). Расчет выполняют непосредственно на графике (рис. 7). Для этого каждое событие делят на 4 сектора, в которых указываются все необходимые для расчета данные о работе (рис. 8).
Рис. 7. Пример расчета сетевого графика секторным методом
Рис. 8. Условные обозначения сетевого графика
Сначала определяют ранние начала работ и записывают в левые секторы событий. Ранние начала работ, выходящих из первого события, принимают равными нулю. Раннее начало любой другой работы равно наибольшей из сумм ранних начал и продолжительностей предшествующих работ, т. е. наибольшему раннему окончанию:
.
Раннее начало работ, выходящих из первого события, равно нулю (речь идет о рабочих днях). Их раннее окончание равно сумме начала и продолжительности, следовательно 
, 
, 
. Рассматриваем по порядку каждое событие и в левом секторе записываем максимальное значение ранних окончаний работ, которые к нему подходят, что будет являться ранним началом работ, из него выходящих. В нижнем секторе в числителе записываем номер события, через которое к данному событию идет самый длинный путь (max t РО ). В конечном событии в правом секторе записываем позднее окончание, равное max 
. Это число соответствует дню окончания строительства и равно длине критического пути. Вычитая из него продолжительность работ, получим поздние начала работ, и если из события выходят несколько работ, то в правом секторе пишем минимальное значение из поздних начал, что будет являться поздним окончанием работ, к нему подходящих. Позднее начало (цифра в правом секторе) у первого события должно быть равно нулю. Разница значений правого и левого сектора дает нам величину общих резервов событий, которые записываются в знаменателе нижнего сектора. На этом расчет графика секторным методом заканчивается.
Пример определения раннего начала для работ 4–5, 4–6, 4–7:
;
.
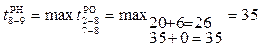
Таким образом, последовательно от исходного события до завершающего определяются все ранние начала работ. Завершающее событие рассматривается как начальное событие условной работы с нулевой продолжительностью.
Поздние окончания работ определяются справа налево, причем позднее окончание завершающих работ равно наибольшему из ранних их окончаний. Так,
.
Позднее окончание записывается в правом секторе завершающего события (в примере (см. рис. 7) завершающее событие имеет номер 9).
Позднее окончание любой работы сетевого графика равно наименьшей из разностей поздних окончаний последующих работ и их продолжительностей:
.
Все работы, входящие в одно событие, имеют одинаковое позднее окончание.
Частный резерв времени работы на графике определить несложно. Следует к раннему началу работы (цифра в левом секторе предшествующего события рассматриваемой работы) прибавить продолжительность работы и полученное значение раннего окончания отнять от раннего начала работ последующих (цифра в левом секторе события, к которому подходит рассматриваемая работа):
; 
;
.
Общий резерв работы равен разнице позднего окончания работы (цифра в правом секторе события, к которому подходит рассматриваемая работа) и раннего окончания работы:
;
Общий резерв работы можно получить, сложив общий резерв события, к которому подходит работа, с частным резервом рассматриваемой работы:
.
Выделим критический путь: начиная от последнего события, он пройдет по событиям с нулевым общим резервом через номера, указанные в числителе нижнего сектора. Критический путь пройдет по работам 1–2–4–7–9.
После всех необходимых расчетов можно построить масштабную модель проектируемого объекта (сетевой график в привязке к календарю) и эпюру движения рабочих (рис. 9) с целью подсчета потребности в ресурсах. При этом местоположение любого события определяет сумма раннего окончания и частного резерва работ, подходящих к рассматриваемому событию, или день раннего начала работ, выходящих из этого события. Привязка идет по рабочим дням. На работах (стрелках) откладывается частный резерв и ставится граница продолжительности и частного резерва (рис. 10).
Рис. 9. Построение эпюры движения рабочих
Рис. 10. Условное обозначение работ на масштабном сетевом графике
Над стрелкой пишут число рабочих. Проекция стрелки (работы) на горизонтальную ось равна сумме продолжительности работы и ее частного резерва (например, длина стрелки, обозначающей работу 3–4, равна
t3–4 + r3–4 = 7 + 9 = 16 дн, см. рис. 9). Если работа не имеет продолжительности (пунктирная стрелка — холостая связь), то ее горизонтальная проекция равна частному резерву (например, проекция работы 2–7). Если же и его нет, то стрелка графика вертикальна и проектируется в точку (работа 7–8).
Следует помнить, что вертикальный масштаб при построении сетевого графика не соблюдается. Местоположение события по вертикали выбирается из соображения удобства (чтобы не было пересечения стрелок) и наглядности. Продолжительности работ под стрелками можно не писать, так как любая работа проектируется на шкалу времени, что указывает на день ее начала и окончания.
Когда сетевой график вычерчен в горизонтальном масштабе, над стрелками указывают потребность в ресурсах (в данном примере это — рабочие): рабочих, материалах, капвложениях и др. Затем по методу вертикального суммирования производят построение эпюры и выполняют ее оптимизацию за счет частных и общих резервов времени [2].