Тема 6 Сетевые графики строительства.
1.Сущность и значение метода сетевого планирования и управления. Основные элементы сетевого графика.
2.Общие принципы построения сетевого графика. Параметры сетевого графика.
3.Аналитический и графический расчет сетевого графика. Оптимизация сетевого графика. 4.Планирование и управление строительным производством на основе сетевых графиков.
1.Сущность и значение метода сетевого планирования и управления. Основные элементы сетевого графика.
Сетевой график – схематическое изображение процесса строительства одного объекта или комплекса объектов, в котором в наглядной форме показывается последовательность выполнения работ и приводятся как технологические, так и организационные их взаимосвязи.
Метод сетевого планирования помогает устанавливать зависимость продолжительности строительства от сроков выполнения отдельных видов работ.
Сетевая модель позволяет:
— четко отобразить структуру проекта и установить взаимосвязь отдельных разделов;
— прогнозировать критические работы;
— более эффективно использовать ресурсы;
— по-новому подойти к учету и отчетности в строительстве и др.
Основные элементы сетевого графика:
работа
 |
 |
конечное
событие
начальное
событие
Фиктивная
 |  |
 |
1.работа – производственный процесс, требующий затрат трудовых, материальных ресурсов, а также времени (сплошная линия со стрелкой наимен.работы )
продолжит., число раб. в смену
2.событие – начало или окончание одной либо нескольких работ. Каждому событию присваивается номер (код). Все работы ограничиваются двумя событиями. Изображается кружками. Событие бывает начальное и конечное.
3.ожидание – это организационный или технологический перерыв между работами, не требующий затрат ресурсов, но занимающий время (например, естественная сушка штукатурки).
4.зависимость (фиктивная работа) – не связана с расходом ресурсов времени и вводится для отражения взаимосвязей между реальными работами. Показывается пунктирной линией со стрелкой
5.путь – непрерывная линия, характеризующая продолжительность работ от начального до конечного события в сетевом графике. Длина пути – это сумма продолжительностей работ, находящихся на данном пути.
В сетевом графике между начальным и конечным событиями может быть несколько путей. Путь, имеющий наибольшую продолжительность, называется критическим (обозначается двумя сплошными линиями ), а работы, входящие в состав критического пути – критическими.
2.Общие принципы построения сетевого графика. Параметры сетевого графика.
Построение сетевого графика ведется по определенным правилам:
1. Направление стрелок – слева направо. Код начального события меньше кода конечного события.
2. Графики должны иметь простую форму, по возможности без пересечения векторов. Большинство работ следует изображать горизонтальными линиями.
3. На графике не должно быть «тупиков» (замкнутых контуров).
4. Между двумя событиями может быть только одна работа.
5. Если после окончания двух работ можно начинать третью, а по окончании каждой из них – другие работы, то показываются зависимости между событиями.
6. Не допускаются события, из которых не выходит ни одна работа (кроме конечного).
Сетевые графики имеют временные параметры:
Предшествующая работа Рассматриваемая работа Последующая работа
 |
Ранее начало работы БПозднее окончание работы А
Работа А Работа Б
 |
 |
 |
Номер предшествующего события, через которое к данному событию
идет максимальный путь
3. Ткр – критический путь
Работы, у которых r = 0, R= 0 – входят в состав критического пути.
Построение сетевого графика: пример. Модель производственного процесса
Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При управлении проектами такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.
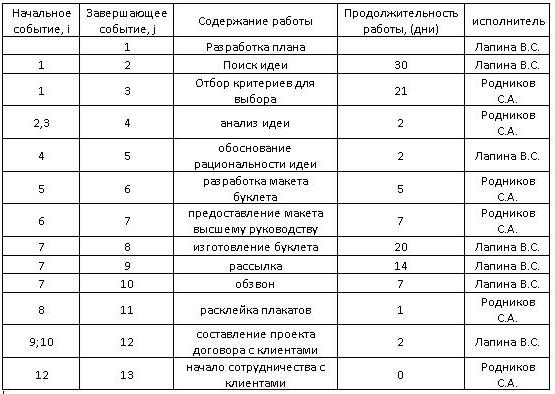
Исходные данные
Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.
Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.
Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:
Построение матрицы
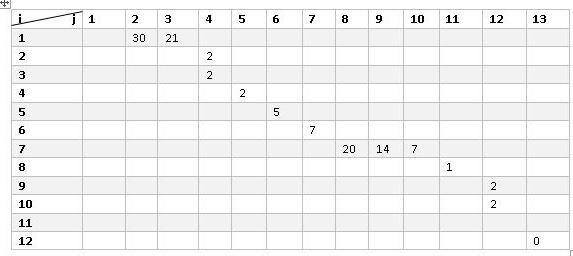
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
Основные элементы, используемые для сетевого графика
Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:
Работа может выполниться в трех состояниях:
— Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.
— Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.
Основные принципы построения
Правила построения сетевых графиков заключаются в следующем:
Построение сетевого графика. Пример
Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.
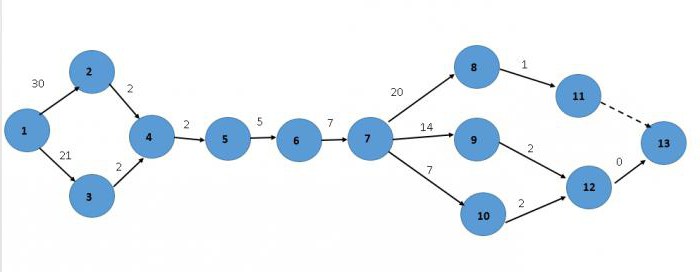
Начинаем с первого события. Из него выходят два – второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:
Критические значения
Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.
Критический путь – это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:
30+2+2+5+7+20+1 = 67 дней
Таким образом, критический путь равен 67 дням.
Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную рисует схемы. Программа для построения сетевых графиков – это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы:
Практика построения сетевого графика
Представим себе ситуацию развития проекта капитального строительства на производственном предприятии. Проект успешно инициирован и полным ходом идут работы по его планированию. Сформирована и утверждена иерархическая структура работ, план по вехам принят. Разработан первичный вариант календарного плана. Поскольку задача оказалась достаточно масштабной, куратор принял решение о разработке еще и сетевой модели. Расчет сетевого графика в прикладном аспекте его исполнения является предметом настоящей статьи.
Перед стартом моделирования
Методологический базис сетевого проектного планирования представлен на нашем сайте несколькими статьями. Я лишь сошлюсь на две из них. Это материалы, посвященные этапу сетевого планирования проекта в целом и непосредственно моделированию сетевого графика проекта. Если в ходе повествования у вас будут возникать вопросы, просмотрите ранее представленные осмысления, основная суть методологии в них изложена. В настоящей статье мы рассмотрим небольшой пример локальной части комплекса строительно-монтажных работ в рамках значительной проектной реализации. Расчеты и моделирование будем выполнять методом «вершина-работа» и классическим табличным способом («вершина-событие») с применением МКР (метода критического пути).
Построение сетевого графика мы начнем на основе первой итерации календарного плана, выполненного в форме диаграммы Ганта. Для целей наглядности предлагаю не учитывать отношения предшествования и максимально упростить последовательность действий. Хотя на практике такое бывает редко, представим в нашем примере, что операции выстроены в последовательность вида «окончание-начало». Ниже вашему вниманию представляются две таблицы: выписка из списка работ проекта (фрагмент из 15-ти операций) и список параметров сетевой модели, необходимый для представления формул.
Пусть вас не пугает обилие элементов. Построение сетевой модели и расчет параметров достаточно просто выполнить. Важно тщательно подготовиться, иметь под рукой иерархическую структуру работ, линейный график Ганта – в общем, все, что дает возможность определиться с последовательностью и взаимосвязями действий. Еще в первые разы выполнения графика я рекомендую иметь перед собой формулы расчета требуемых значений. Они представлены ниже.
Что нам потребуется определить в ходе построения графика?
Последовательность действий по моделированию
Шаг первый
Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.
В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.
Шаг второй
Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.
Шаг третий
Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.
Шаг четвертый
Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности. Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика.
Дополнительные расчеты модели
Выполнение расчета общего резерва текущей операции производится путем вычитания из значения позднего начала раннего начала или из позднего окончания раннего окончания (см. схему расчета выше). Общий (полный) резерв показывает нам возможность начала текущей работы позже или увеличения продолжительности на длительность резерва. Но нужно понимать, что пользоваться полным резервом следует с большой осторожностью, потому что работы, стоящие от текущего события дальше остальных, могут оказаться без запаса времени.
Помимо полных резервов в сетевом моделировании оперируют также и частными или свободными резервами, которые представляют собой разницу между ранним началом последующей работы и ранним окончанием текущей. Частный резерв показывает, есть ли возможность сдвинуть ранее начало операции вперед без ущерба для начала следующей процедуры и всему графику в целом. Следует помнить, что сумма всех частных резервных значений тождественна полному значению резерва для рассматриваемого пути.
Главной задачей выполнения вычислений различных параметров является оптимизация сетевого графика и оценка вероятности выполнения проекта в срок. Одним из таких параметров является коэффициент напряженности, который показывает нам уровень сложности реализовать работу в намеченный срок. Формула коэффициента представлена выше в составе всех расчетных выражений, применяемых для анализа сетевого графика.
Коэффициент напряженности определяется как разница между единицей и частного от деления полного резерва времени работы на разницу длительности критического пути и особого расчетного значения. Это значение включает ряд отрезков критического пути, совпадающих с максимально возможным путем, к которому может быть отнесена текущая операция (i-j). Далее помещен расчет частных резервов и коэффициентов напряженности работ для нашего примера.
Коэффициент напряженности варьируется от 0 до 1,0. Значение 1,0 устанавливается для работ, находящихся на критическом пути. Чем ближе значение некритической операции к 1,0, тем труднее удержаться в плановых сроках ее реализации. После того, как значения коэффициента по всем действиям графика посчитаны, операции, в зависимости от уровня этого параметра, могут быть отнесены к категории:
Оптимизация сетевой модели, нацеленная на сокращение общей продолжительности проекта, как правило, обеспечивается следующими мероприятиями.
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.