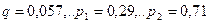Применение теории игр к строительству противолавинных сооружений
Второй пример связан со строительством противолавинных сооружений.
Использование горной территории в рекреационных целях всегда связано с проблемой защиты от лавин и селей: зданий, канатных дорог, используемых для катания склонов, а также проживающих в этих районах жителей и горнолыжников, катающихся по данным склонам. В целях безопасности часто требуется строительство противолавинных сооружений, а для этого нужны значительные материальные затраты. Именно поэтому необходимо создание карт лавинной опасности территории, связанной с рекреационной деятельностью. Карты лавинной опасности помогают прояснить в целом лавинную ситуацию района. Одной из задач для составления карт является оценка объема снега, который может быть потенциально вовлечен в движение и, в результате, принести материальный ущерб.
Предположим теперь, что карты лавинной опасности имеются и на них отмечены участки, подвергающиеся лавинной опасности один раз во много лет. Проанализируем данную ситуацию. Если организация, которая контролирует данную ситуацию, располагает большим количеством материальных средств, то никакой научной задачи не возникает. Можно построить (с избытком) на всех склонах противолавинные сооружения, создать рекламу о безопасности катания на данных склонах в виду наличия противолавинных сооружений и получать соответствующую ситуации выгоду. Проблема возникает (а это более реальная жизненная ситуация), когда имеется ограниченное количество материальных средств. Стоит ли создавать на всех участках противолавинные сооружения при ограниченном количестве материальных средств? Какие выбрать участки? Такая задача может быть отнесена к области конфликтных ситуаций, и аппарат теории игр может помочь наилучшим образом распределить имеющиеся материальные средства для создания противолавинных сооружений.
Рассматривая строительство противолавинных сооружений, мы имеем дело с игрой m* n. Это означает, что природа имеет m стратегий (лавиноопасных склонов), а человек имеет n стратегий (в частности, он может построить на склоне противолавинное (одно или несколько) сооружение). Данная игра содержит случайные ходы, так как мы не знаем точно время, когда сойдет лавина.
Для решения задачи в области смешанных стратегий введем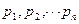 
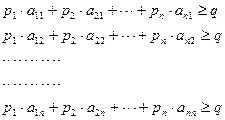
— относительные частоты применения стратегий и запишем следующую систему уравнений:
(2.26)
Разделим левые части уравнения (2.26) нa q и введем обозначения:
(2.27)
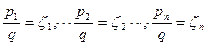
Перепишем уравнение (2.27) в следующем виде:
(2.28)
Так как желание человека заключается в увеличении выигрыша, следовательно:
должна быть минимальной. Для решения такого рода задачи разработан математический аппарат линейного программирования. Решение уравнений (2.28) дает возможность вычислять цену игры q.
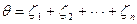
Перераспределяя различными способами сумму М, отпущенную на строительство противолавинных сооружений, человек изменяет коэффициенты матрицы.
Вычисляя в каждом конкретном случае цену игры q, можно найти оптимальный вариант, который дает возможность распределить средства таким образом, чтобы выигрыш со стороны человека был максимален.
Рассмотрим в качестве иллюстрирующего примера два лавиноопасных склона, по которым спускаются лавины мощностями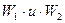 
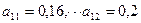
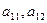
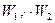
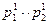
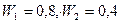
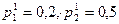
. Будем считать, что ущерб, производимый лавиной, прямо пропорционален ее мощности и равен: 
. (Коэффициенты 
получены путем перемножения мощностей лавин 
на вероятности их схода 
. Для расчета использовались следующие значения: 
, 
).
Предположим, что суммы противолавинных средств М, имеющейся в наличии, хватает ровно для того, чтобы создать противолавинные сооружения, преграждающие путь лавине мощностью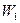 
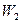
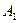
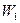
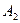
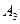
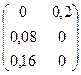
. Допустим, что 50% средств М достаточно для полной защиты от лавины мощностью 
. Рассмотрим три варианта (три стратегии) со стороны человека. При первой стратегии ( 
) все средства М тратятся на преграждение пути лавины мощностью , при этом вторая лавина может двигаться беспрепятственно. Суть второй стратегии ( 
) в следующем: средства делятся пополам для создания противолавинных сооружений первой и второй лавин. При этом вторая лавина будет полностью закрыта. Согласно третьей стратегии ( 
) все средства тратятся на создание сооружения для второй лавины. Матрица игры будет иметь следующий вид:
(2.29)
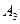
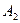
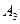
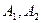
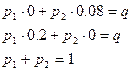
Так как каждый элемент стратегии больше или равен элементу стратегии , то стратегия заведомо невыгодная, и ее можно вычеркнуть. Решая систему уравнений, содержащую две стратегии человека ( 
):
(2.30)
Данное решение означает следующее: для получения выигрыша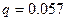 
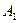
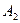
надо в 29 % пользоваться стратегией , а в 71 % стратегией .
Конечно, сход лавин – явление вероятностное, тем не менее, в данном случае вторая стратегия явно предпочтительнее.
Дата добавления: 2015-06-26 ; Просмотров: 529 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Теория игр: 5 простых примеров популярных игровых стратегий
Теория игр занимается тем, что изучает способы сделать лучший ход и в результате получить как можно больший кусок выигрышного пирога, оттяпав часть его у других игроков. Она учит подвергать анализу множество факторов и делать логически взвешенные выводы. Я считаю, её нужно изучать после цифр и до алфавита. Просто потому что слишком многие люди принимают важные решения, основываясь на интуиции, тайных пророчествах, расположении звёзд и других подобных. Я тщательно изучил теорию игр, и теперь хочу рассказать вам о её основах. Возможно, это добавит здравого смысла в вашу жизнь.
1. Дилемма заключенного
Берто и Роберт были арестованы за ограбление банка, не сумев правильно использовать для побега угнанный автомобиль. Полиция не может доказать, что именно они ограбили банк, но поймала их с поличным в украденном автомобиле. Их развели по разным комнатам и каждому предложили сделку: сдать сообщника и отправить его за решетку на 10 лет, а самому выйти на свободу. Но если они оба сдадут друг друга, то каждый получит по 7 лет. Если же никто ничего не скажет, то оба сядут на 2 года только за угон автомобиля.
Каждый заключенный — игрок, и выгода каждого может быть представлена в виде «формулы» (что получат они оба, что получит другой). Например, если я ударю тебя, моя выигрышная схема будет выглядеть так (я получаю грубую победу, ты страдаешь от сильной боли). Поскольку у каждого заключенного есть два варианта, мы можем представить результаты в таблице.
Практическое применение: Выявление социопатов
Здесь мы видим основное применение теории игр: выявление социопатов, думающих лишь о себе. Настоящая теория игр — это мощный аналитический инструмент, а дилетантство часто служит красным флагом, с головой выдающим человека, лишенного понятия чести. Люди, делающие расчеты интуитивно, считают, что лучше поступить некрасиво, потому что это приведет к более короткому тюремному сроку независимо от того, как поступит другой игрок. Технически это правильно, но только если вы недальновидный человек, ставящий цифры выше человеческих жизней. Именно поэтому теория игра так популярна в сфере финансов.
Настоящая проблема дилеммы заключенного в том, что она игнорирует данные. Например, в ней не рассматривается возможность вашей встречи с друзьями, родственниками, или даже кредиторами человека, которого вы посадили в тюрьму на 10 лет.
Хуже всего то, что все участники дилеммы заключенного действуют так, как будто никогда не слышали ней.
А лучший ход — хранить молчание, и через два года вместе с хорошим другом пользоваться общими деньгами.
2. Доминирующая стратегия
Это ситуация, при которой ваши действия дают наибольший выигрыш, независимо от действий оппонента. Что бы ни происходило — вы всё сделали правильно. Вот почему многие люди при «дилемме заключенного» считают: предательство приводит к «наилучшему» результату независимо от того, что делает другой человек, а игнорирование действительности, свойственное этому методу, заставляет всё выглядеть супер-просто.
Большинство игр, в которые мы играем, не имеет строго доминирующих стратегий, потому что иначе они были бы просто ужасны. Представьте, что вы всегда делали бы одно и то же. В игре «камень-ножницы-бумага» нет никакой доминирующей стратегии. Но если бы вы играли с человеком, у которого на руках надеты прихватки, и он мог показать только камень или бумагу, у вас была бы доминирующая стратегия: бумага. Ваша бумага обернет его камень или приведет к ничьей, и вы не сможете проиграть, потому что соперник не может показать ножницы. Теперь, когда у вас есть доминирующая стратегия, нужно быть дураком, чтобы попробовать что-нибудь другое.
3. Битва полов
Игры интереснее, когда у них нет строго доминирующей стратегии. Например, битва полов. Анджали и Борислав идут на свидание, но не могут выбрать между балетом и боксом. Анджали любит бокс, потому что ей нравится, когда льется кровь на радость орущей толпе зрителей, считающих себя цивилизованными только потому, что они заплатили за чьи-то разбитые головы.
Борислав хочет смотреть балет, потому что он понимает, что балерины проходят через огромное количество травм и сложнейших тренировок, зная, что одна травма может положить конец всему. Артисты балета — величайшие спортсмены на Земле. Балерина может ударить вас ногой в голову, но никогда этого не сделает, потому что ее нога стоит гораздо дороже вашего лица.
Каждый из них хочет пойти на своё любимое мероприятие, но они не хотят наслаждаться им в одиночестве, таким образом, получаем схему их выигрыша: наибольшее значение — делать то, что им нравится, наименьшее значение — просто быть с другим человеком, и ноль — быть в одиночестве.
Некоторые люди предлагают упрямо балансировать на грани войны: если вы, несмотря ни на что, делаете то, что хотите, другой человек должен подстроиться под ваш выбор или потерять все. Как я уже говорил, упрощённая теория игр отлично выявляет глупцов.
Практическое применение: Избегайте острых углов
Конечно, и у этой стратегии есть свои значительные недостатки. Прежде всего, если вы относитесь к вашим свиданиям как к «битве полов», она не сработает. Расстаньтесь, чтобы каждый из вас мог найти человека, который ему понравится. А вторая проблема заключается в том, что в этой ситуации участники настолько не уверены в себе, что не могут этого сделать.
По-настоящему выигрышная стратегия для каждого — делать то, что они хотят, а после, или на следующий день, когда они будут свободны, пойти вместе в кафе. Или же чередовать бокс и балет, пока в мире развлечений не произойдет революция и не будет изобретен боксерский балет.
4. Равновесие Нэша
Равновесие Нэша — это набор ходов, где никто не хочет сделать что-то по-другому после свершившегося факта. И если мы сможем заставить это работать, теория игр заменит всю философскую, религиозную, и финансовую систему на планете, потому что «желание не прогореть» стало для человечества более мощной движущей силой, чем огонь.
Практическое применение: сначала думайте
В этом вся суть теории игр. Не обязательно выиграть и тем более навредить другим игрокам, но обязательно сделать лучший для себя ход, независимо от того, что подготовят для вас окружающие. И даже лучше, если этот ход будет выгоден и для других игроков. Это своего рода математика, которая могла бы изменить общество.
Интересный вариант этой идеи — распитие спиртного, которое можно назвать Равновесием Нэша с временной зависимостью. Когда вы достаточно много пьете, то не заботитесь о поступках других людей независимо от того, что они делают, но на следующий день вы очень жалеете, что не поступили иначе.
5. Игра в орлянку
В орлянке участвуют Игрок 1 и Игрок 2. Каждый игрок одновременно выбирает орла или решку. Если они угадывают, Игрок 1 получает пенс Игрока 2. Если же нет — Игрок 2 получает монету Игрока 1.
Выигрышная матрица проста…
…оптимальная стратегия: играйте полностью наугад. Это сложнее, чем вы думаете, потому что выбор должен быть абсолютно случайным. Если у вас есть предпочтения орла или решки, противник может использовать его, чтобы забрать ваши деньги.
Конечно, настоящая проблема здесь заключается в том, что было бы намного лучше, если бы они просто бросали один пенс друг в друга. В результате их прибыль была бы такой же, а полученная травма могла бы помочь этим несчастным людям почувствовать что-то, кроме ужасной скуки. Ведь это худшая игра из существующих когда-либо. И это идеальная модель для серии пенальти.
Практическое применение: Пенальти
В футболе, хоккее и многих других играх, дополнительное время — это серия пенальти. И они были бы интереснее, если бы строились на том, сколько раз игроки в полной форме смогут сделать «колесо», потому что это, по крайней мере, было бы показателем их физических способностей и на это было бы забавно посмотреть. Вратари не могут чётко определить движение мяча или шайбы в самом начале их движения, потому что, к огромному сожалению, в наших спортивных состязаниях роботы все еще не участвуют. Вратарь должен выбрать левое или правое направление и надеяться, что его выбор совпадет с выбором противника, бьющего по воротам. В этом есть что-то общее с игрой в монетку.
Однако обратите внимание, что это не идеальный пример сходства с игрой в орла и решку, потому что даже при правильном выборе направления вратарь может не поймать мяч, а нападающий может не попасть по воротам.
Итак, каково же наше заключение согласно теории игр? Игры с мячом должны заканчиваться способом «мультимяча», где каждую минуту игрокам один на один выводится дополнительный мяч/шайба, до получения одной из сторон определенного результата, который был показателем настоящего мастерства игроков, а не эффектным случайным совпадением.
В конце концов, теория игр должна использоваться для того, чтобы сделать игру умнее. А значит лучше.