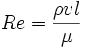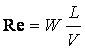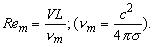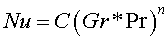Теория подобия в строительстве

Реферат: Основы теории подобия (метод обобщенных переменных)

Основы теории подобия (метод обобщенных переменных)

Методы исследования технологических процессов

Теория подобия. Виды подобия

Основные положения теории подобия (теоремы подобия)

Методы исследования технологических процессов

Исследования процессов, протекающих в технологических установках, установление закономерностей их протекания, нахождение зависимостей, необходимых для их анализа и расчета, можно проводить разными методами: теоретическим, экспериментальным, подобия.

Теоретический метод основан на составлении и решении системы дифференциальных уравнений, описывающих процесс. Дифференциальные уравнения описывают целый класс однородных по своей сущности явлений (процессов), поэтому для выделения конкретного явления необходимо ввести определенные ограничения, которые однозначно будут характеризовать данное явление. Эти дополнительные условия называются условиями однозначности. Условия однозначности включают в себя: геометрическую форму и размеры системы, т.е. аппарата, канала и т.д.; физические свойства веществ, участвующих в процессе; начальные условия (начальную температуру, начальную скорость и т.д.); граничные условия, например скорость жидкости у стенок канала, равную нулю.

Однако многие процессы химической технологии так сложны, что удается лишь составить систему дифференциальных уравнений и установить условия однозначности. Решить эти уравнения известными в математике методами не представляется возможным.

Экспериментальный метод позволяет на основе опытных данных получить эмпирические уравнения, описывающие данный процесс. Сложности экспериментального метода заключаются в необходимости проведения большого количества опытов на реальных технологических установках. Это связано с большими затратами средств и времени. Вместе с тем результаты проведенных экспериментов будут справедливы только для тех условий, для которых они получены, и не могут быть с достаточной надежностью перенесены на процессы, аналогичные изученным, но протекающие в других аппаратах.

Метод теории подобия позволяет с достаточной для практики точностью изучать сложные процессы на более простых моделях, обобщать результаты опытов и получать закономерности, справедливые не только для данного процесса, но и для всей группы подобных процессов. При моделировании процессов можно вместо дорогостоящих трудоемких опытов на промышленных установках проводить исследования на моделях значительно меньших размеров, а вместо зачастую опасных и вредных веществ использовать безопасные модельные вещества, опыты проводить в условиях, отличных от производственных. Кроме того, материальную модель можно заменить физической схемой (моделью), отражающей существенные особенности данного процесса. Поэтому в данном учебном пособии наиболее подробно будет рассмотрена теория подобия.

Теория подобия. Виды подобия

Метод обобщенных переменных составляет основу теории подобия. Одним из основных принципов теории подобия является выделение из класса явлений (процессов), описываемых общим законом (процессы движения жидкостей, диффузии, теплопроводности и т.п.), группы подобных явлений.

Подобными называются такие явления, для которых отношения сходственных и характеризующих их величин постоянны.

Различают следующие виды подобия: геометрическое; временное; физических величин; начальных и граничных условий.

(1)

Рис. 1. Условия подобия в натуре (a) и в модели (б)

теория подобие переменная обобщенный

При соблюдении геометрического и временного подобия константа подобия скоростей k_υ определяется из соотношений

(2)

Подобие физических величин предполагает, что для двух любых сходственных точек натуры и модели, размещенных подобно в пространстве и во времени, соотношение физических величин (μ,ρи т.д.) является величиной постоянной:

(3)

Подобие начальных и граничных условий заключается в том, что для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие так же, как и для других сходственных точек натуры и модели.

Рассмотренные константы подобия постоянны для различных сходственных точек подобных систем, но могут изменяться в зависимости от соотношения размеров натуры и модели, т. е. если имеется другая модель, подобная натуре, константы подобия будут другими.

Если подобные величины выразить в относительных единицах, т.е. в виде отношений сходственных величин в пределах одной системы (натуры или модели), то получим инварианты подобия:

(4)

Инварианты подобия, выраженные отношением разнородных величин, называются критериями подобия. Критерии подобия обозначаются начальными буквами имен ученых, которые внесли большой вклад в развитие данной области знаний.

Критерии подобия безразмерны, их значения для разных точек системы могут быть различными, но для сходственных точек подобных систем они одинаковые и не зависят от относительных размеров натуры и модели.

Критерии подобия имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами, силами и т.п., оказывающими влияние на протекание данного процесса.

Критерии подобия могут быть получены для любого процесса, если известны уравнения, описывающие этот процесс.

Основные положения теории подобия (теоремы подобия)

Основные положения теории подобия заключены в теоремах подобия, которые лежат в основе практического применения теории подобия.

Теорема была сформулирована Ньютоном. Она устанавливает, что единственным количественным условием подобия процессов является равенство критериев подобия натуры и модели.

Отсюда очевидно, что отношение критериев одной системы (натуры) к критериям другой подобной ей системы (модели) всегда равно 1. Например,

Если отношение констант подобия равно 1, оно носит название индикатора подобия и указывает на равенство критериев подобия.

Следовательно, у подобных явлений индикаторы подобия равны 1.

Первая теорема подобия указывает, какие величины следует измерять при проведении опытов, результаты которых требуется обобщить: надо измерять те величины, которые входят в критерии подобия.

Обычно критериальное уравнение записывается в виде зависимости определяемого критерия подобия от определяющих критериев подобия:

где А, т, п — эмпирические показатели.

Третья теорема подобия (теорема Киринчен-Гухмана): явления подобны, если их определяющие критерии равны.

Следствием равенства определяющих критериев подобия является равенство и определяемых критериев для натуры и модели, поэтому полученная на модели в результате опытов критериальная зависимость будет справедлива для всех подобных процессов, в том числе и для протекающих в промышленной установке. При этом следует учитывать, что полученные уравнения надежно можно использовать только в тех интервалах изменения переменных, которые были использованы при проведении опытов.

Таким образом, для исследования технологических процессов методом подобия необходимо:

1. выбрать дифференциальное уравнение и условия однозначности, описывающие данный процесс; затем путем преобразования найти критерии подобия;

2. опытным путем с помощью моделей установить зависимость между критериями подобия; полученное обобщенное уравнение будет справедливым для всех подобных процессов в пределах изменения определяющих критериев подобия.

Преобразование дифференциальных уравнений методом теории подобия проводится в следующем порядке:

2. полученные коэффициенты перед членами уравнения для соблюдения тождественности приравниваются;

3. в полученных индикаторах подобия константы подобия заменяются соответствующими отношениями величин, и полученные комплексы являются критериями подобия.

В табл. 1 приведены основные критерии гидродинамического подобия, которые будут равны для сходственных точек натуры и модели, если они подобны.

Название: Основы теории подобия (метод обобщенных переменных) Раздел: Рефераты по экономико-математическому моделированию Тип: реферат Добавлен 03:53:33 03 июня 2011 Похожие работы Просмотров: 9858 Комментариев: 17 Оценило: 7 человек Средний балл: 4.1 Оценка: 4 Скачать

Критерий	Выражение критерия	Характеристика критериев	Единицы измерения входящих в критерии подобия величин
Кинематический (критерий Рейнольдса)	Rе=υl/ν= υlρ/μ	Характеризует меру соотношения сил инерции и сил трения
Гравитационный (критерий Фруда)	Fr =υ 2 /gl	Характеризует меру соотношения сил инерции и сил тяжести
Гидравлического сопротивления (критерий Эйлера)	Еu =∆p/ρ υ 2	Характеризует меру соотношения сил гидростатического давления и сил инерции
Гомохронности	Но =υ τ/l	Характеризует неустановившееся движение жидкости

f (Rе, Но, Fr, Еu) = 0 (8)

Уравнение (8) является обобщенным критериальным уравнением гидродинамики. Все критерии уравнения (8), кроме критерия Ей, являются определяющими, так как они составлены из величин, входящих в условия однозначности. Критерий Эйлера, в который входит величина ∆р, являющаяся целью расчета, будет определяемым критерием.

Еu = f (Rе, Но, Fr) или

где А,c,т,п- эмпирические показатели.

В ряде случаев уравнение (19) дополняют геометрическим симплексом l / d :

где b- эмпирический показатель.

При установившемся движении критерий Но исключается из критериального уравнения:

В случае, если скорость движения жидкости не определена, в расчеты вводят производные или модифицированные критерии подобия, составленные из основных критериев. В этих критериях подобия неизвестная величина υ заменяется другими величинами, которые сравнительно легко определяются экспериментально или аналитически.

Возьмем отношение критериев Rе и Fr:

(12)

(13)

Источник

Основы подобия и моделирования

В основе методов моделирования лежит учение о подобии, основы которого заложены еще И Ньютоном.

Чтобы получить корректные результаты необходимо обеспечить подобие модели и натуры, т. е.

а) подобие геометрических свойств систем;

б) пропорциональность физических констант, имеющих существенное значение в изучаемом процессе;

в) подобие начального состояния систем;

г) подобие условий на границах систем в течение всего рассматриваемого периода процесса;

д) равенство определяющих критериев, при этом определяющими критериями подобия являются те, которые имеют существенное значение в изучаемом процессе.

При характеристике того или иного механического процесса механическое подобие может быть определено заданием переходных множителей или масштабов для длин (геометрическое подобие), для времени (кинематическое подобие) и для масс (динамическое подобие).

Для двух подобных систем условиегеометрического подобия состоит в том, что все размеры пространства, занятого системой в модели, и размеры отдельных элементов модели изменены в определенное число mL раз по сравнению с соответствующими размерами натуры:

Условие кинематического подобия этих систем состоит в том, что любые сходственные точки (частицы) систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени Т, отличающиеся постоянным множителемmТ

Условие динамического подобия систем состоит в том, что массы любых сходственных частиц этих систем отличаются друг от друга постоянным множителемmМ

Особенности объектов геомеханики состоят в том, что при заданном геометрическом масштабе моделирования (mL = Lм / Lн) для обеспечения механического подобия модели и натуры необходимо отказаться в модели либо от равенства sм = sн, либо от равенства gм = gн, либо от равенства обоих показателей.

Если сохранить в модели равенство напряжений натуре (другими словами, равенство механических свойств материала модели и натуры), т.е. условие sм =sн, то необходимо обеспечить, чтобы объемный вес материала был больше в число раз, обратное геометрическому масштабу.

Например, при геометрическом масштабе модели mL = Lм / Lн = 1/100 объемный вес материала модели должен быть равен

Условие (10.4) можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес (100gн в приведенном случае при mL = 1/100) с помощью инерционных сил, которые могут быть созданы, например, путем вращения модели в центрифуге при соответствующем значении центробежной силы. Этот метод был предложен в 1932 г. профессорами Г. И. Покровским и Н. Н. Давиденковым и носит название метода центробежного моделирования.

Если же в модели применить некоторые искусственные материалы, механические характеристики которых ниже соответствующих характеристик моделируемых горных пород, т. е. отказаться от равенства sм = sн, то для обеспечения условий механического подобия модели и натуры необходимо

При моделировании системы в соответствующем геометрическом масштабе продолжительность тех или иных процессов обычно изменяется. В связи с этим существенно важное значение имеет вопрос о масштабе времени при моделировании, который в общем случае определяется, исходя из приведенного выше условия кинематического подобия двух систем (10.2).

В тех случаях, когда на моделях воспроизводят сразу несколько процессов, масштабы времени для отдельных из них могут оказаться неодинаковыми В таких случаях масштаб времени устанавливают, исходя из соблюдения подобия в протекании лишь тех процессов, которые в решаемой задаче являются основными и не учитывают малозначащие элементы.

Нагружение физических моделей осуществляется:

* созданием усилий на контуре модели при помощи механических и гидравлических домкратов или заданием деформаций контура посредством жёстких ограничителей;

* собственным весом модели массива;

* посредством центробежных сил, возникающих в центрифуге;

* с помощью сил сопротивления сдвигу, как это делается в моделях с фрикционной базой.

В анализе систем, имеющих границы раздела фаз, появляются внутренние характерные масштабы, связанные с взаимодействием внешних полей и поверхностных эффектов. В газожидкостных потоках важнейшая характеристика этих эффектов – коэффициент поверхностного натяжения σ, Н/м. Основные гидродинамические взаимодействия поверхностного натяжения возникают с гравитационными силами, обусловленными разностью плотностей фаз (сила Архимеда), с мерой g(ρ’–ρ’’), Па/м, динамическим напором с мерой ρU2, Па, и вязким трением, мерой которого является динамическая вязкость μ, Па*с, или кинематическая вязкость ν, м2/с.
При наличии свободных границ возникают также локальные взаимодействия подъёмной (архимедовой) силы и вязкого трения. Из этих величин можно образовать несколько масштабов, существенных в анализе термогидродинамики газожидкостных систем.
Вводя в классические критерии подобия внутренние линейные масштабы, можно образовать новые критерии, не зависимые от внешних геометрических характеристик потока. Такую операцию проводят в теории пограничного слоя при образовании чисел Рейнольдса. Существенно, что в данном случае результат получается нетривиальным и приводит к качественно новым безразмерным параметрам.
Так, для гравитационно-вязкого течения жидкой плёнки число Нуссельта удобно писать в форме

то есть строить его по внутреннему линейному масшабу.
Введя в число Нуссельта линейный масштаб капиллярно-гравитационного взаимодействия, получим ещё одну его форму

Критерии подобия, необходимые условия физического подобия двух явлений, например явлений, имеющих место для натурного объекта и его модели. Критерии подобия, состоящие в равенстве для рассматриваемых явлений некоторых безразмерных величин, называются характеристическими числами. Иногда критериями подобия называются сами эти числа. Ими являются число Маха, число Рейнольдса, число Прандтля, число Струхаля, число Эйлера, число Фруда и другие.

Число Рейнольдса – безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.

Число Рейнольдса определяется следующим соотношением:

где ρ – плотность среды, v – характерная скорость, l – характерный размер, μ – динамическая вязкость среды.

Переход от ламинарного к турбулентному режиму происходит по достижении так называемого критического числа Рейнольдса Rekp. При Re Rekp возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе .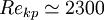

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.

Критерий назван в честь выдающегося английского физика О. Рейнольдса (1842–1912), автора многочисленных пионерских работ по гидродинамике.

Критерий Рейнольдсa (критерий гидродинaмического подобия):

где W – скорость потока; L – определяющий размер; V – кинематическая вязкость среды.

Уравнение индукции магнитного поля имеет очень важную интерпретацию в магнитной гидродинамике. Действительно, отношение по порядку величины второго члена в правой стороне этого уравнения к первому равно

Здесь V – некоторая характерная скорость задачи (например, скорость невозмущенного потока, набегающего на обтекаемое тело), а L – характерный размер (например, размер обтекаемого тела). Величина nm называется магнитной вязкостью. Число Rem внешне похоже на число Рейнольдса в классической гидроаэромеханике (только вместо кинематической вязкости жидкости n = m /r в рассматриваемом случае в знаменателе стоит магнитная вязкость) и играет такую же важную роль, как и число Рейнольдса в гидроаэромеханике.

Rem >1 сильно влияет на распределение магнитного поля, а, следовательно, и на распределение всех остальных электродинамических величин. Кроме того, есть теорема, что поток соленоидального вектора, которым является магнитное поле (div B = 0), через некоторую поверхность S в жидкости, ограниченную жидким контуром С, остается со временем постоянным. Физически это означает, что никакая силовая линия магнитного поля во время движения не может покинуть поверхность S через контур С. Это свойство электропроводных жидкостей и газов в случае Rem>>1 называется условием «вмороженности» магнитных силовых линий в электропроводную среду. В гидроаэромеханике аналогом являются вихревые линии, которые при некоторых условиях могут быть «вморожены» в жидкость (одна из теорем Гельмгольца о вихрях). Случай Rem>>1 чаще всего осуществляется в различных физических проблемах, встречающихся в условиях космического пространства. Это связано с тем, что обычно в этих условиях характерные размеры L приводят к очень большим значениям магнитного числа Рейнольдса.

В качестве примера приведем обтекание магнитосферы Земли солнечным ветром. Скорость солнечного ветра в районе орбиты Земли равна, в среднем, V

4•107см/сек, характерный размер обтекаемой магнитосферыL

6,4•109 см (RE – радиус Земли), nm

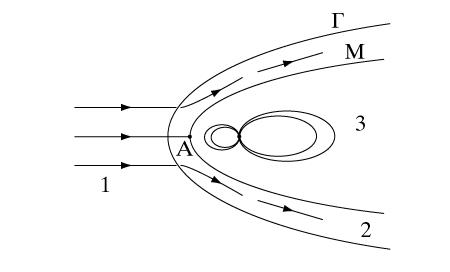
1011>>1. Таким образом, при обтекании Земли солнечным ветром осуществляется случай Rem>>1, т.е., в силу принципа «вмороженности», солнечный ветер не может проникнуть в магнитосферу Земли, а обтекает ее, поджимая магнитосферу с подветренной стороны и вытягивая ее в хвостовой части, как показано на рис. 1. На этом рисунке область «1» представляет собой невозмущенный солнечный ветер, Г – головная ударная волна, М – так называемая магнитопауза, отделяющая солнечный ветер за головной ударной волной от магнитосферы Земли, А – точка торможения солнечного ветра, в которой скорость равна нулю, область «2» заполнена солнечным ветром, параметры которого за ударной волной отличаются от параметров в области «1», область «3» – магнитосфера Земли, куда не проникает солнечный ветер. Исследования с помощью космических аппаратов обнаружили, что хвост магнитосферы Земли может вытягиваться вплоть до орбиты Луны.

Качественная картина обтекания магнитосферы Земли солнечным ветром

В случае Rem 0.7) в этом равенстве аргументом является произведение Gr*Pr, называемое числом Рэлея Ra. Для определения зависимости Nu = f(Gr, Рr) предложено много эмпирических корреляционных формул: большинство из них имеет вид зависимости

Дата добавления: 2015-05-26 ; Просмотров: 3322 ; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник